Desde que o mundo é mundo e mesmo sem saber que calculava, o homem já calculava.
Maneiras para se trabalhar de forma lúdica:
Trabalhamos, aqui, a parte 3 da divisão da Matemática: Geometria e Formas, não só por ser nuclear para o aprendizado dos demais conteúdos como por permear todas as modalidades da Educação Básica: Educação Infantil, Ensino Fundamental e Ensino Médio.
Muitos conhecem o Tangram, um quebra-cabeça chinês, de origem milenar. Seu nome original é: Tch´ i Tch´ iao Pan, significa as sete tábuas da argúcia. Ao contrário de outros quebra-cabeças ele é formado por apenas sete peças com formas geométricas resultantes da decomposição de um quadrado, são elas:
2 triângulos grandes;
2 triângulos pequenos;
1 triângulo médio
1 quadrado
1 paralelogram
|  |
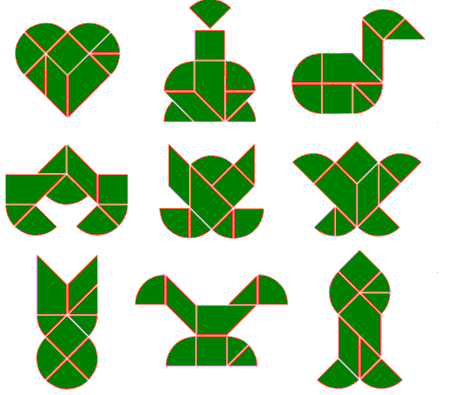
Com estas peças é possível criar e montar cerca de 1700 figuras entre animais, plantas, pessoas, objetos, letras, números, figuras geométricas entre outras. Veja:
O professor pode iniciar a apresentação deste jogo-material pedagógico contando uma lenda sobre o Tangram, assim:Um jovem chinês despedia-se de seu mestre, pois iniciaria uma grande viagem pelo mundo. Nessa ocasião, o mestre entregou-lhe um espelho de forma quadrada e disse:
Com esse espelho você registrará tudo o que vir durante a viagem,
para mostrar-me na volta.
O discípulo surpreso, indagou:
Mas mestre, como, com um simples espelho, poderei eu lhe mostrar tudo o que encontrar durante a viagem?
No momento em que fazia esta pergunta, o espelho caiu-lhe das mãos, quebrando-se em sete peças.
Então o mestre disse:
Agora você poderá, com essas sete peças, construir figuras para ilustrar o que viu durante a viagem.
Com o uso do tangram o professor pode trabalhar:
identificação,
comparação,
descrição,
classificação,
desenho de formas geométricas planas,
visualização e representação de figuras planas,
exploração de transformações geométricas através de decomposição e composição de figuras,
compreensão das propriedades das figuras geométricas planas,
representação e resolução de problemas usando modelos geométricos
noções de áreas
frações
Esse trabalho permite o desenvolvimento de algumas habilidades – IMPORTANTES PARA A AQUISIÇÃO DE CONHECIMENTO S EM OUTRAS ÁREAS – tais como:
Por último, o professor precisa se conscientizar que este quebra-cabeça tem sido utilizado como material didático nas aulas de Artes e precisa estar cada vez mais presente nas aulas de Matemática. O trabalho com oTangram deve iniciar visando a exploração das peças e a identificação das suas formas.
Logo depois, se passa à sobreposição e construção de figuras dadas a partir de uma silhueta, nesse caso, cabe ao aluno reconhecer e interpretar o que se pede, analisar as possibilidades e tentar a construção. Durante todo esse processo, a criança precisa analisar as propriedades das peças do Tangram e da figura que se quer construir, se detendo ora no todo de cada figura, ora nas partes.
A filosofia do Tangram é de que um todo é divisível em partes, as quais podem ser reorganizadas num outro todo, como a própria concepção de Malba Tahan sobre a matemática. As regras do principal jogo proposto no trabalho com Tangram consistem em usar as sete peças em qualquer montagem de reprodução de figuras, apresentadas em silhueta, utilizando as sete peças, colocando-as lado a lado sem sobreposição.
Atualmente, se tem trabalhado bastante com o Ovogran, um QCG - Quebra-cabeças Geométrico - mais complexo, de construção complicada, cuja construção transcrevo do livro "Quebra-cabeças Geométricos e formas planas" de Ana Maria M. F. Kaleff:
"sobre uma folha de papel cartão, desenha-se um triângulo retângulo isósceles (com os catetos medindo, por exemplo, quatro centímetros). A seguir, traça-se um segmento de reta contendo a hipotenusa desse triângulo do seguinte modo: marca-se, a partir de cada vertice da hipotenusa, um segmento com medida igual à do lado do cateto do triângulo retângulo construído. Desenha-se uma semicircunferência tendo este segmento por diâmetro. Então traça-se a mediatriz deste diâmetro no semiplano que não contém a semicircunferência. Sobre a mediatriz traça-se um ponto cuja distância ao diâmetro seja igual á metade do cumprimento do diâmetro. A seguir, une-se este ponto às extremidades do diâmetro da semicircunferência, formando-se um triângulo retângulo cuja hipotenusa é o diâmetro. Então, constrói-se um arco centrado em uma das extremidades do diâmetro cuja medida do raio é igual à medida deste. Prolonga-se um dos catetos do triângulo retângulo cuja hipotenusa é o diâmetro até que encontre o arco traçado. Então deve-se repetir este traçado para a outra extremidade do diâmetro. Com centro no vértice do ãngulo de 90º deste triângulo retângulo e raio igual à medida do segmento que une este vértice ao arco considerado, traça-se um arco unindo os dois últimos arcos desenhados. A seguir, traça-se um segmento de reta perpendicular ao diâmetro da semicircunferência, ligando o vértice do ângulo reto do primeiro triângulo construído à semicircunferência." Parece complicado para professores polivalentes, então, para facilitar, você pode tirar uma cópia do diagrama abaixo e, simplesmente, imprimir, ampliar, colar em cartolina ou papel cartão, plastificar e dar asas à imaginação de sua garotada! Outra alternativa, são os modelos em EVA, vendidos em lojas de brinquedos pedagógicos. Seus alunos vão adorar se aventurar.

Observação:
1.Devemos problematizar o cotidiano, superar o pronto e acabado.
2.Diariamente enfrentamos problemas que nos obrigam a pensar e organizar informações na busca de soluções. É aquela que exige uma maneira matemática de pensar, isto é, uma situação em que são aplicados os conhecimentos matemáticos para encontrar a solução.
3.Uma das finalidades de estudar matemática é aprender como se resolvem problemas, indo além da simples busca de uma resposta. É uma atividade motivadora, criativa e desafiadora.
4.Os erros e as dúvidas dos alunos devem ser encarados como um momento de construção do conhecimento e não como incapacidade. Para o aluno, o erro fornece informações sobre o seu conhecimento, desenvolvimento e raciocínio. Para o professor, a análise do erro é um ponto de partida para a avaliação das estratégias adotadas e para a escolha de novas atividades.
5.Muitas vezes o erro na Matemática está atrelado à dificuldade de interpretação do texto ou por falhas na compreensão do sistema de numeração decimal.
6.Quando o erro acontecer devemos evitar confrontar o verdadeiro e o falso e sim pedir ao aluno para justificar o raciocínio usado na resolução do problema. Mais importante que a criança acertar é saber justificar como chegou a um resultado.
7.Os jogos, pelo seu aspecto lúdico, podem motivar e despertar o interesse do aluno, tornando a aprendizagem mais atraente. a partir de erros e acertos e da necessidade de análise sobre a eficiência de cada estratégia, construída para alcançar a vitória no jogo, estimula-se o desenvolvimento do raciocínio reflexivo daqueles que jogam.
8.O Tangram, como jogo ou como arte, possui um forte apelo lúdico e oferece àquele que brinca um envolvente desafio. Cada vez mais presente nas aulas de Matemática, as formas geométricas que o compõem, permitem que os professores vejam neste material a possibilidade de inúmeras explorações.
9.Que a matemática é subdividida por "partes" como: aritmética, álgebra, geometria, mecânica e astronomia.
10.Todas essas partes se confundem, se apóiam e se auxiliam mutuamente, assim, não há necessidade para ansiedades e fobias em seu aprendizado ou ensino.
Bibliografia:
Kaleff, Ana Maria; Monteiro Rei, Dulce; Garcia, Simone dos Santos. Quebra-cabeças Geométricos e formas planas. Editora da Universidade Federal Fluminense – Niterói/RJ, 2002.
Toledo, Marília e Mauro. Didática da Matemática: como dois e dois: a construção da matemática. São Paulo: FTD, 1997.
.gif)
.gif)



.gif)



.gif)



.gif)